How to train your Lipschitz Network
What are Lipschitz Networks?
In my endeavours to try to make AI more safe and understandable, I make use of neural networks which I call “Lipschitz Networks” (even though this term is not consistently used in literature).
Lipschitz networks constrain the gradient p-norm $|\nabla_x f(x)|_p$ of your network with respect to the inputs to a maximum of your choice, lets say 1. In practice, there are multiple ways to do this. The requirements for a suitable implementation are as follows:
- $|\nabla_x f(x)|_p \leq 1$.
- Can approximate every $f(x)$ to arbitrary precision if 1. is fulfilled
The Layerwise Constraint
One very safe or deterministic way of implementing requirement 1 is constraining the jacobian operator norm of each layer with respect to the input. In fully connected networks, the weight matrices coincide with the jacobian, so it is convenient to constrain these directly, layerwise: $|W^i|_p \leq 1 \ \forall i$
However, a layerwise constraints can overdo the trick. Since the Lipschitz constant of a (fully connected) neural network is determined by the product of the jacobians and the lipschitz constants of the activations, a layerwise constraint easily accumulates into something that is much smaller than 1 and cannot recover the “full gradient”. (Anil et al., 2019) refer to this as gradient norm attenuation.
The GroupSort activation
The specific problem is the fact that the usual activation functions, while being Lipschitz-1, cannot maintain a maximum allowed gradient everywhere. For instance, if one neuron has a preactivation of $< 0$, ReLU will result in a gradient of 0 there and a possible $| \nabla_x f(x) | = 1$ is unachievable. (Anil et al., 2019) show this very nicely by trying to fit a layerwise constrained network with ReLU activation to the absolute value function. Spoiler: It does not work.
So they went ahead and derived a new activation function: GroupSort. It sorts
the preactivations within n subgroups of the input. Example: GroupSort(1) is the
full sort operation, GroupSort(d/2) is the MaxMin operation.
Since it is merely a permutation, it maintains gradient 1 everywhere, while being
a sufficient nonlinearity to serve as activation. Together with a specific constraint,
they are able to prove universal approximation of GroupSort Lipschitz networks!
The weight norm constraint to achieve p-normed Lipschitzness is:
Training the Lipschitz Network
Ok, so let us train a Lipschitz network for some binary classification task! For training data, let’s use the two-moons dataset. Using BCE as loss and Adam as optimizer, we can train a Lipschitz network with a Lipschitz constant of 1. We immediately see that the network is unable to achieve a good classification performance.
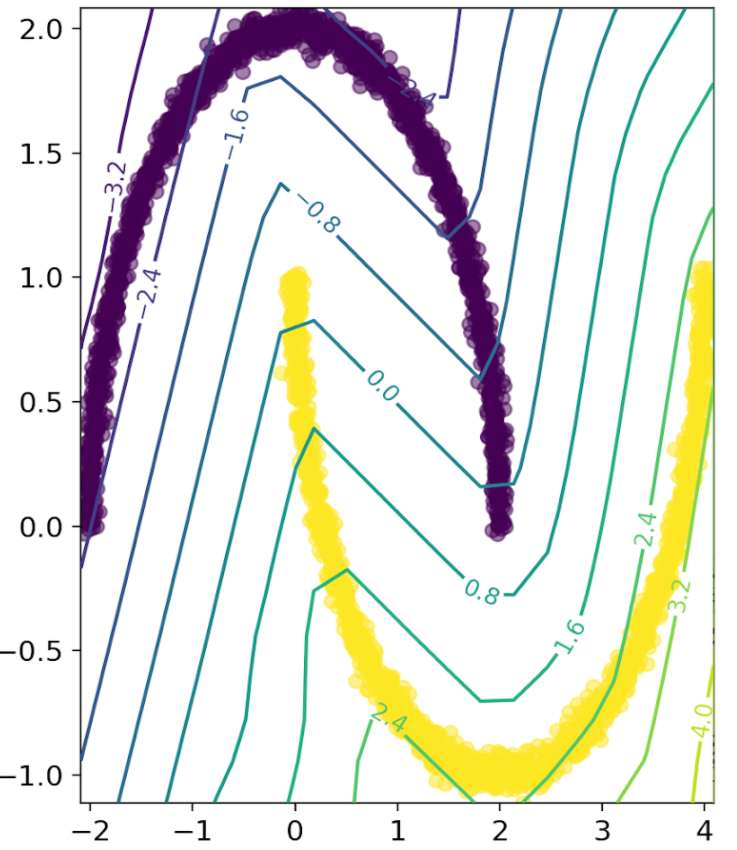
The reason for this is not that the gradient is too constrained. In fact, we should be able to achieve perfect classification performance with any Lipschitz constant > 0, because the decision frontier is defined only by the sign of the output (or the sign of output - 0.5 if it’s in [0,1]), and the sign is scale invariant. So why does this not work?
Recall how BCE works: It tries to maximize the margins, i.e. get the output for
class 0 as close as possible to 0 and the output of class 1 as close as possible
to 1. With a sigmoid as output activation, this means unbounded increase for
the preactivations to minimize BCE.
In unconstrained networks, that is fine and actually desirable. In a Lipschitz
network, it is unadvisable to concentrate on margin maximization because, when
the gradient is bounded, the objective may clash with the actual goal of
classification: Maximizing accuracy. A loss function that cares about margin
maximization up until a certain point is much better suited here: Hinge loss!
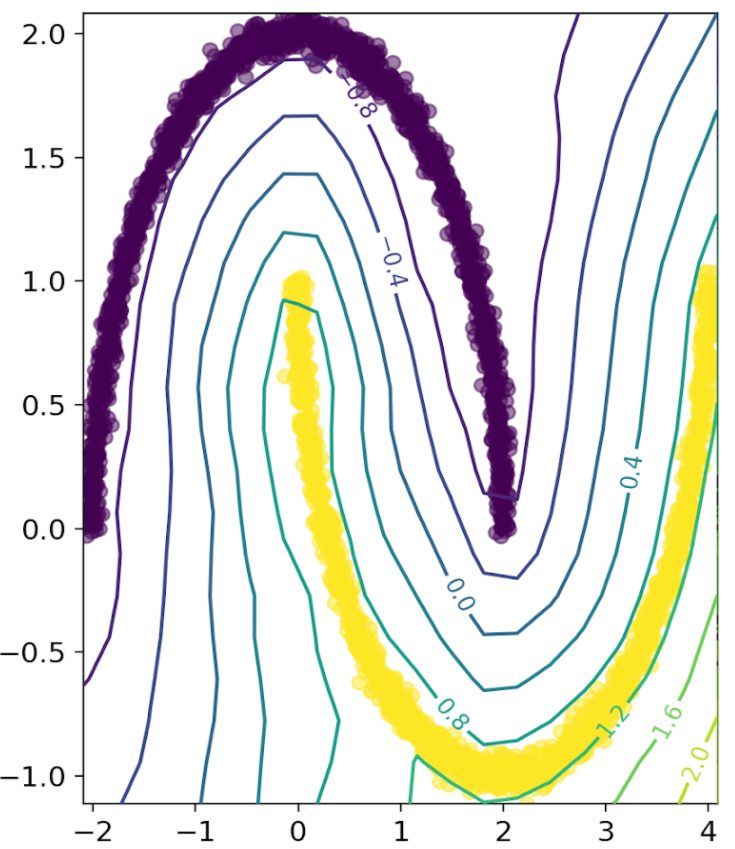
Hinge loss does not assign a penalty to training data outside of a margin of specified size, so the Lipschitz network can concentrate its efforts on optimizing the decision frontier.
More on this when I find more time.
References
- Anil, C., Lucas, J., & Grosse, R. (2019). Sorting out Lipschitz function approximation.